Delaunay Triangulation Implementation

Delaunay Triangulation

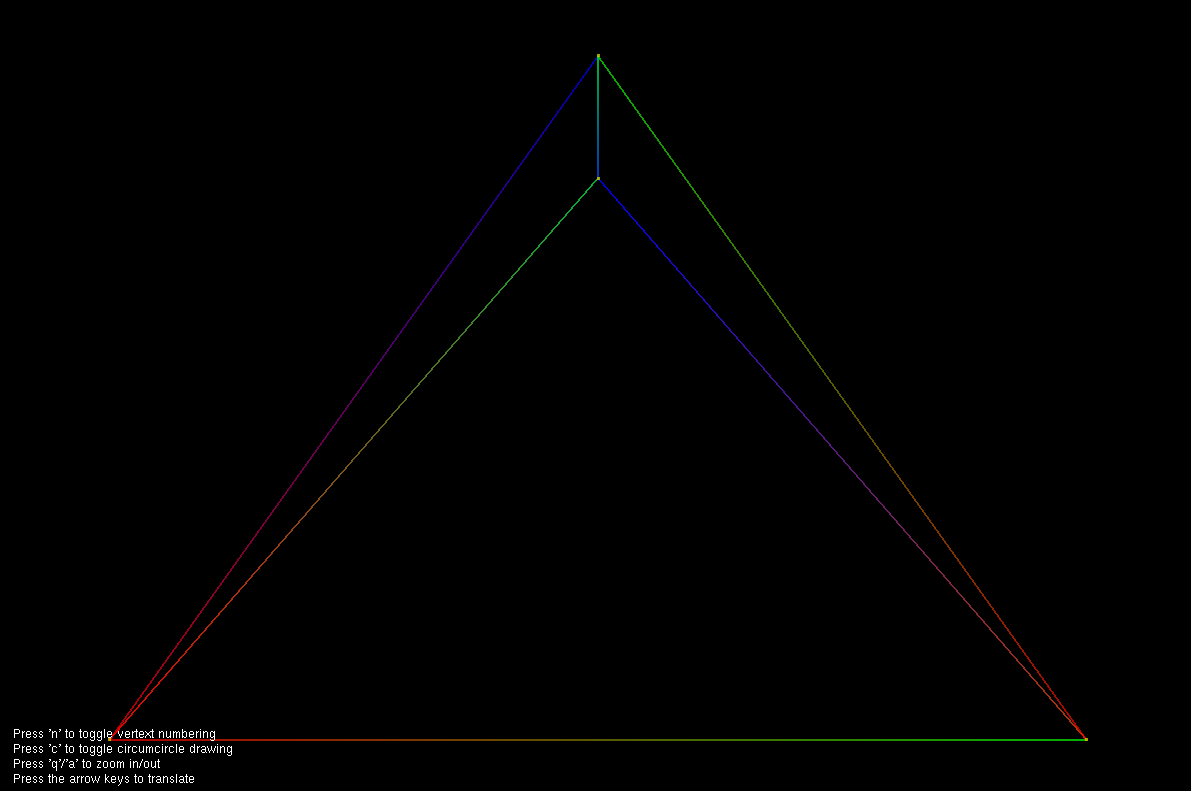
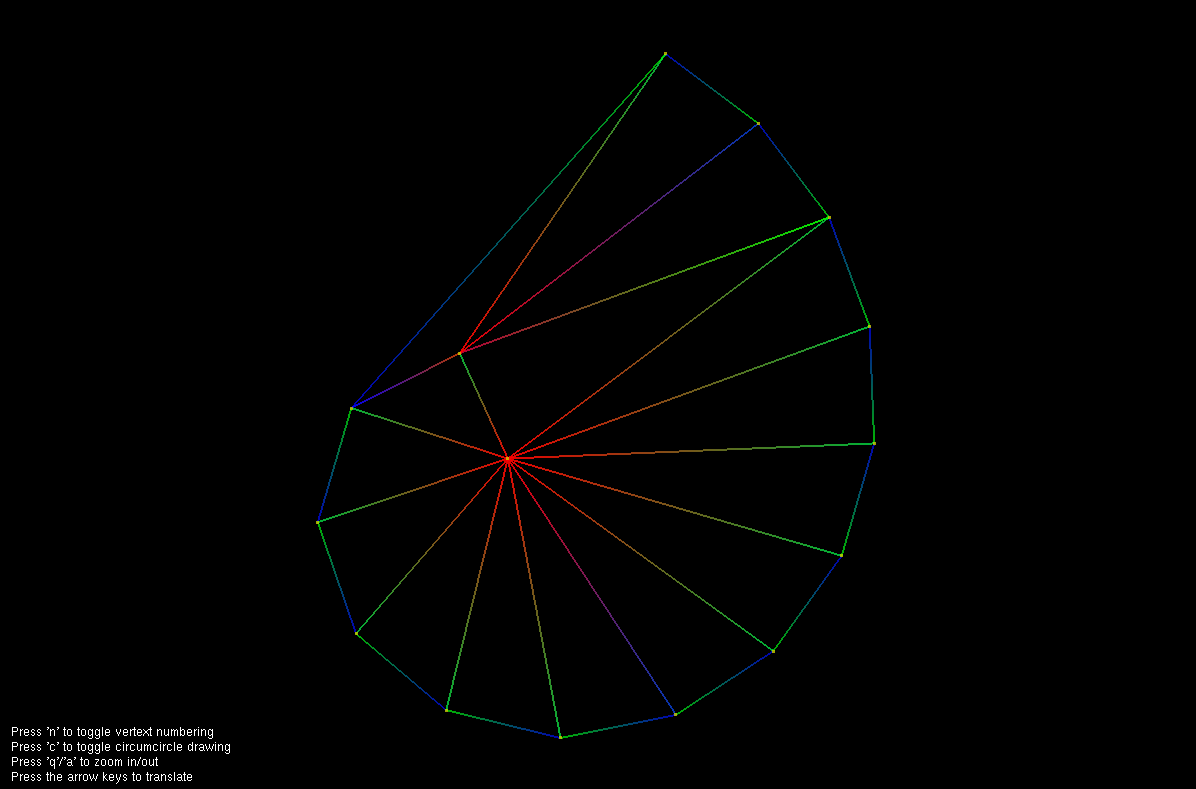
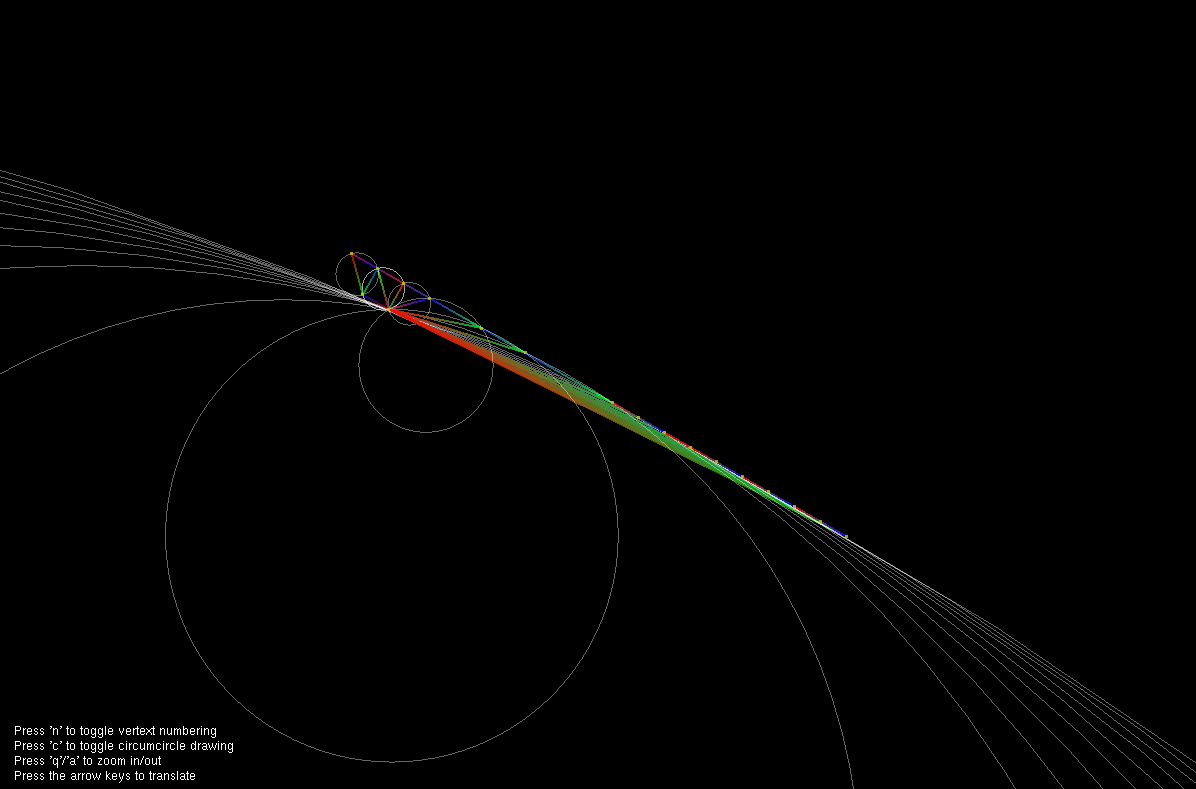
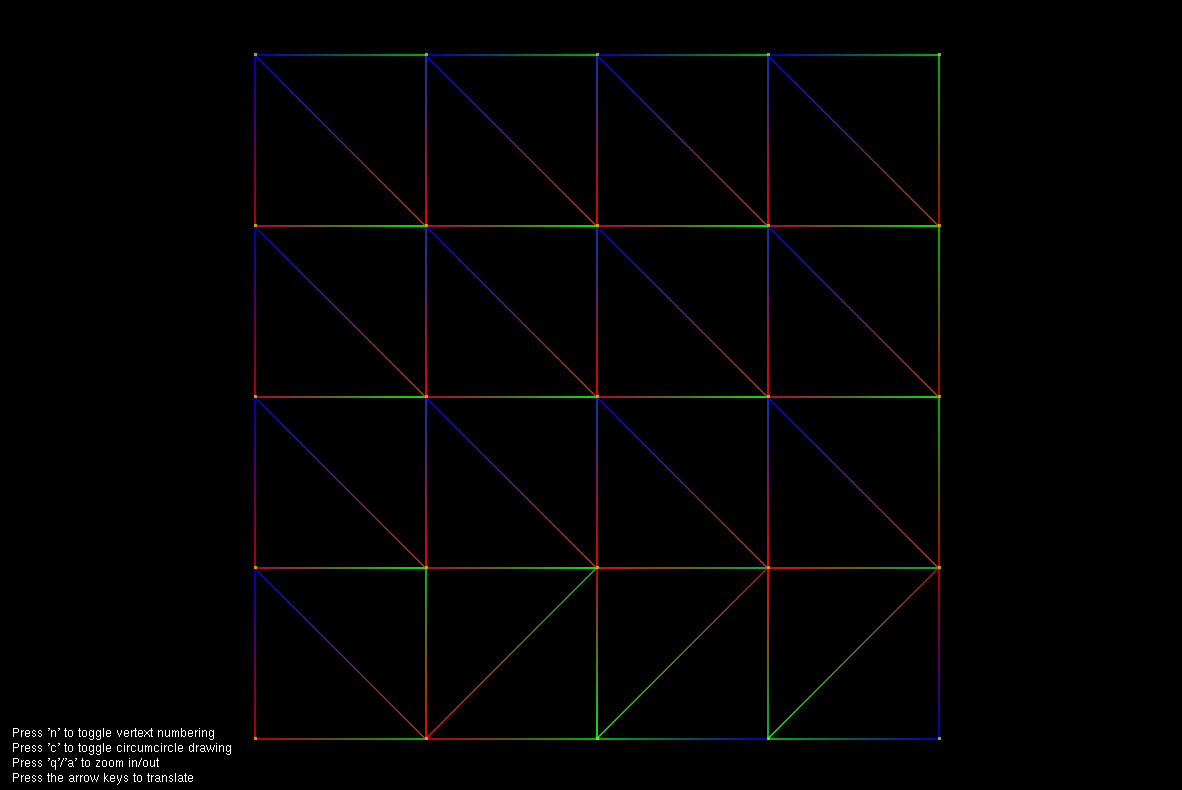
In mathematics and computational geometry, a Delaunay triangulation for a set P of points in a plane is a triangulation DT(P) such that no point in P is inside the circumcircle of any triangle in DT(P). Delaunay triangulations maximize the minimum angle of all the angles of the triangles in the triangulation; they tend to avoid skinny triangles. The triangulation is named after Boris Delaunay for his work on this topic from 1934.

System

- Macbook Air (CPU 1.7 GHz Intel Core i5, MEM 4GB 1333 MHz DDR3)
- Mac OS X (Version 10.7.3)
- C++ on XCode (Version 4.2.1)
- OpenGL for visualization. No other external libraries and codes are used.

Algorithms

- Triangulation : (Random) Incremental insertion
- Data structure : Blanford, Blelloch, Cardoze, and Kadow, Compact Representations + Ghost vertex
- Walking point location

How to Run

$ ./DelaunayTri [input_file_name] [-random] [-step]

Result Screenshots

Input file : 4.node (4 vertices, 0.00002 sec)

Input file : box.node (12 vertices, 0.00006 sec)

Input file : spiral.node (15 vertices, 0.00007 sec)

Input file : flag.node (18 vertices, 0.00011 sec)

Input file : grid.node (25 vertices, 0.00015 sec)

Input file : dots.node (100 vertices, 0.0006 sec)

Input file : 633.node (633 vertices, 0.00617 sec)

Input file : ttimeu10000.node (10000 vertices, 0.18539 sec)

Input file : ttimeu100000.node (100000 vertices, 6.59373 sec)

Input file : ttimeu1000000.node (1000000 vertices, 251.8904 sec)
Input file : ttimec10000.node (10000 vertices, 0.2006 sec)

Input file : ttimec100000.node (100000 vertices, 15.17289 sec)
Input file : ttimec1000000.node (778404 vertices, 1521.76435 sec)
Input file : ttimeg10000.node (10000 vertices, 0.60725 sec)
Input file : ttimeg100000.node (100000 vertices, 28.54346 sec)
Input file : ttimeg1000000.node (1000000 vertices, 762.6159 sec)